Recibido: 08/06/2023 Aceptado: 29/06/2023 Publicado: 29/07/2023

Introduction

Synchronization is a phenomenon that has many examples in natural processes, such as the perfectly coincided oscillation of two pendulum clocks hanging from the same base [11], the synchronous firing of neurons [2],[5] or the symmetry of animal gaits [12]. As in these examples, interconnections in the systems achieve synchronization without external interference; We speak of self-synchronization. Additionally, we find numerous examples in different mechanical and electrical structures, such as transmitter-receiver systems, quadruped robot movements [3] etc. where the synchronization is achieved by external inputs and couplings, because of which we speak of controlled synchronization. This article focuses on the controlled synchronization of robot manipulators. We find many applications in production processes where robotic systems' synchronous behavior is necessary for producing equal-quality parts. In surgery, new minimal invasive robotic systems have been developed [8] that require the synchronization of the robot with the trajectory that the operating surgeon generates.

While the control of robot manipulators is a classical control problem, the problem of the synchronization of robots has not received much attention. We can find some approaches in [10] where the system's parameters are estimated by an observer using only angular positions. Using those estimates, an adaptive control strategy is realized. However, this technique requires the exact knowledge of the system's dynamics, which results in a non-robust approach. Therefore, in a realistic case, there is no knowledge of the friction’s terms, parameter variations, etc.

This article assumes that the robot system's parameters and dynamics are uncertain and that only the angular positions can be measured. Departing from the ideas presented in [4] we use the proposed robust nonlinear control scheme for the Multiple Input Multiple Output (MIMO) case. The methodology achieves the synchronization of an arbitrary number of robots despite structural and parametric differences of the robots, and it is robust against external perturbations, friction, and parameter variations. After transforming the system into a linearizable canonical form, the uncertain dynamics and parameters are lumped into a new state. This new state is unknown, as well as the angular velocities; because of this, a high-gain observer estimates it. With the estimated states, a stabilizing controller is implemented based on linearization. Finally, the robots are connected in a mutual pattern that achieves the synchronization between the robots and concerns a trajectory given by the user.

Materials and Methods

Let us consider a robotic manipulator that consists of  links and has  rotatory degrees of freedom that create the generalized angular positions . We assume that it is possible to generate  torques ,  in the link connections, for example, with the help of electrical motors, hydraulic systems, etc. It was presumed that it is possible to measure the angular positions of links at each point in time while the availability of the angular velocity was not postulated. The robot's links were modeled as perfectly stiff, i.e., bending and vibration effects were neglected. With the help of the Euler-Lagrange or similar equations, we can derive the following model of a robot with  rotatory degrees of freedom:

Eq. 1

 is the symmetric, positive definite inertia matrix while  represent the Coriolis and centrifugal forces.  denotes the gravity forces, and the friction in the element connections is represented by the function . We decided to use the static friction model that proposed (Hellsen et al., 2000). The following equation represents it:

Eq. 2

 is used to model the viscous friction, while the remaining terms approximate the Coulomb and Stribeck friction effects.

We carry out the following transformation:

Eq. 3

Now (1) becomes a nonlinear  MIMO system, that is characterized by  first order differential equations:

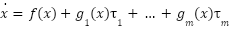
Eq. 4

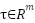With the states , the system input  and the system output . The system is characterized by the function  and the matrix :

Eq. 5

For the synchronization of two or various robotic manipulators, we will presume that every system fulfills the following assumptions:

1. Only the angular positions  can be measured at each point in time, i.e., not all the states  of the system are available.
2. There is no exact knowledge of the structure and the coefficients of , , , and .
3. The robotic manipulators may be strictly different, but they all have the same degrees of freedom and the same inputs.

Numerous synchronization designs exist, such as serial or parallel master-slave models, etc. (Nijmeijer et al., 2003). However, this work will discuss the mutual synchronization pattern, where synchronous behavior is achieved with the interaction between the robots. The robots are arranged in a network, and every robot can be connected to all the other robots. Let us suppose we have a number of   robots. For mutual synchronization the trajectories of reference  with ,  of the robot  for the degree of freedom 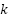 are calculated as follows:

Eq. 6

Where 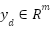 is the desired trajectory given by the user, which is equal for all the robots and has to be smooth.  are the so-called coupling factors. They define how strong the robot  will interact with the robot . High values of the coupling factors will lead to a fast synchronization between the robots, and low values will lead to a fast synchronization of the robots with the desired trajectory .

The synchronization of all robot manipulators is achieved if  for  and . It is straightforward that this is only possible if also  for  and . The synchronization problem can be formulated as designing the interconnections between the robots and creating control feedback for the robots. In the next chapter, we will propose a robust control feedback strategy well-suited for robot mutual synchronization.

Results and Discussion

To implement the proposed feedback scheme, the system has to be transformed on Burnes Isidori Normal Form. Because this transformation requires the knowledge of the relative degree vector, we will use the following definition [7]:

Definition 2: (Relative Degree) The relative degree vector  of an affine MIMO system as in (4) is defined by:

1.  for all 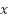 close to  and , ,
2. The matrix  is nonsingular

With this definition, we can find that, for the robot manipulators,  and that the relative degree of every input is . As , the system has full order and, therefore, has no internal dynamics.

Now we can carry out the transformation , , with:

Eq. 7

With this transformation the system (4) is linearizable and becomes:

 =  

Eq. 8

In the case of robot manipulators, the transformation ,  is always a diffeomorphism and thereby  is an invertible transformation. This means that if we can control (8) we can also control (4). The vector  is defined by  and the matrix  by . We find that  and . Thus, the linearizing controller  is called the perfect control. If we choose 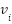 for  as follows

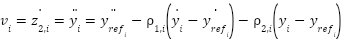
Eq. 9

the outputs of the system can follow any affine vector of trajectories of reference  without any permanent error.

Remark 1: The controller  requires the exact knowledge of all the states  as well as the knowledge of   and  for  at each point in time.

However, as we have assumed in assumption A.2, in the case of the robot manipulators, we have no exact knowledge of the structure and the coefficients of , ,  and  which means that also  and  are uncertain. Besides, according to assumption A.1, only the angular positions  can be measured while the angular velocities  are unknown.

Following the ideas presented in [4], [1]), and [9] where the controller requires only the least prior knowledge about the system (8) and can stabilize the system at the origin or make it follow any affine trajectory. The control scheme does not require the knowledge of  and . The idea is to lump these uncertain terms into a new observable state that can be reconstructed from the available angular positions .

We introduce the new variable vector , which contains the uncertain functions  and  for  :

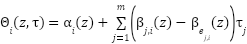
Eq. 10

 is a user-defined approximation of  that has to fulfill . With this we can rewrite the system (8), for :

Eq. 11

Now we augment our system by  additional states  with . In this way (11) becomes:

Eq. 12

Where , in assumption A.1 we have supposed that we have no exact knowledge about all the states . Consequently, the new state vector  is also unknown. To solve this problem, we construct the following high-gain observer that is based on the available states .

Eq. 13

Now we have to choose the coefficients  in such a way that the polynomials ,  have poles with negative real parts.  is a tuning parameter that strongly influences the error dynamics.

Based on the estimates of the uncertainties  and the estimates of  we can construct the following linearizing-like feedback controller

Eq. 14

With the input vector  that is defined as:

Eq. 15

Proposition 1: The robust feedback method consists of the dynamic estimator (13) and the linearizing controller (15), that was constructed using the estimates of  (i.e. ) and  that are provided by the high-gain observer.

Proof: The proof of stability is equal for all the  degrees of freedom. Because of this, we will carry out a parallel proof for all the degrees of freedom, and  will be valid. For the stability of the observer, we define an estimation error 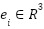 in the following way: 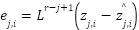,  and 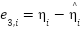. Now, using (12) and (13) we can write the error dynamics  as:

Eq. 16

Or written in Matrix form:

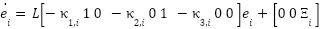
Eq. 17

The matrix  is Hurwitz if the poles of the polynomial  are in the left pane of the complex plane. If this is the case, then, according to Lyapunov, there exists a positive definite and symmetric matrix  such that  where  is the identity matrix of dimension . Now we choose  as Lyapunov function and get:

Eq. 18

If  satisfies  and  for some  and  then  is a bounded function. Let  be some positive constant and . We can write  for the stability of the observer  has to be fulfilled for all .  We can see that the estimation error  depends directly on . As  increases,  and the estimation error bound will decrease. Because of this,  should be chosen as big as possible.

 We conclude: As all  are bounded, if  then  for  and  . With this we conclude, that (13) and (14) yield asymptotical stabilization of the system (8).

To illustrate the proposed control scheme, we will now apply the methodology to the case of a robot manipulator with  rotatory degrees of freedom. With the help of the Euler-Lagrange or similar equations we can calculate , ,  of (1) as follows:

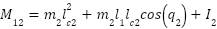
We will use the same friction term 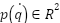 as in (2). Again  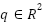are the angular positions of the links while  are the angular velocities and 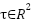 are the torques that are applied to the links. ,  are the lengths of the links and ,  are the distances to their centers of mass. ,  are the masses of the two elements, ,  are their moments of inertia (including the motors, joints, etc.) and 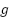 is the acceleration of gravity.

After replacing ,   and  we can rewrite our system (1):

Eq. 19

   Where 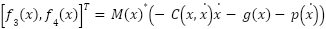. Using Definition 2, we find that the relative degree is . Now we introduce the augmented state vector  and the user-defined approximation of  and get:

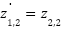
Eq. 20

For the reconstruction of the angular velocities  and the extended state  we construct the high-gain observer:

Eq. 21

With the estimates of (21) we can implement the following controller:

Eq. 22

In order to follow the smooth trajectory of reference , we choose  as:

Eq. 23

Now the coupling factors were chosen as  while the we consider arbitrary initial conditions for ,  and 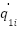, 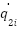. The controller was switched on after 5 seconds, and after 10 seconds, a perturbation torque Nm was applied to both link connections of all the robots.  was turned off after 15 seconds. We chose an arbitrary smooth function for the trajectory . The following variables were chosen equally for all four robots:

Table 1. Parameters of the systems.

In the table  is the high-gain parameter,  is given in meters and  is in .

In Fig. 1, we can see the free oscillation of the uncontrolled robots in the first 5 seconds. After this period, the robots follow the arbitrary, user-given trajectory  with very small errors. In Fig. 2, one can identify the torques generated to compensate for the perturbation.

Figure 1. (a)  and system output 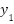. (b)  and system output .

a)

b)

Indeed, note that in Fig. 1, the effect of the perturbation is very low (after 5 and after 10 seconds). This shows that the approach does not require the estimation of the perturbation.

Figure 2. (a) 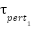 and system input . (b)  and system input .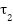

a)

b)

Conclusions

In this work, we have presented a robust control scheme that achieves synchronization of robot manipulators with an arbitrary number of degrees of freedom. It compensates unmodeled dynamics, uncertain or time-varying parameters, and external perturbations and requires only the measurement of the angular positions at each point in time. The central feature of this approach is that the uncertainties are lumped into an extended state, which a high-gain observer reconstructs. Based on this estimation, a linearizing-like control law is implemented that achieves the synchronization in combination with a mutual connection pattern of the robots. The methodology was demonstrated for the case of a 2 DOF robot manipulator and validated by numerical results. The proposed control scheme can also be applied to other mechanical systems, such as robot manipulators with linear degrees of freedom and in combination with other synchronization patterns.

 Conflicts of Interests

The authors solemnly declare that we are not and shall not be in any situation which could give rise to a conflict of interest.

References

[1] R. Femat, R. Jauregui-Ortiz, y G. Solis-Perales, “A chaos-based communication scheme via robust asymptotic feedback”, IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, vol. 48, núm. 10, pp. 1161–1169, oct. 2001, doi: 10.1109/81.956010.

[2] G. Solís-Perales y J. S. Estrada, “A Model for Evolutionary Structural Plasticity and Synchronization of a Network of Neurons”, Comput Math Methods Med, vol. 2021, p. 9956319, 2021, doi: 10.1155/2021/9956319.

[3] Z. G. Zhang, H. KIMURA, y K. TAKASE, “Adaptive Running of a Quadruped Robot Using Forced Vibration and Synchronization”, Journal of Vibration and Control - J VIB CONTROL, vol. 12, pp. 1361–1383, dic. 2006, doi: 10.1177/1077546306070596.

[4] R. Femat, J. Alvarez-Ramírez, y G. Fernández-Anaya, “Adaptive synchronization of high-order chaotic systems: a feedback with low-order parametrization”, Physica D: Nonlinear Phenomena, vol. 139, núm. 3–4, pp. 231–246, may 2000, doi: 10.1016/S0167-2789(99)00226-2.

[5] B. Lading, E. Mosekilde, S. Yanchuk, y Y. Maistrenko, “Chaotic synchronization between coupled pancreatic β-Cells”, Progress of Theoretical Physics Supplement, núm. 139, Art. núm. 139, 2000, doi: 10.1143/PTPS.139.164.

[6] R. H. A. Hensen, M. J. G. van de Molengraft, y M. Steinbuch, “Frequency domain identification of dynamic friction model parameters”, IEEE Transactions on Control Systems Technology, vol. 10, núm. 2, pp. 191–196, mar. 2002, doi: 10.1109/87.987064.

[7] A. Isidori, Nonlinear control systems II. en Communications and control engineering. London: Springer, 1999.

[8] M. Eugster, C. Duverney, M. Karnam, N. Gerig, P. C. Cattin, y G. Rauter, “Robotic Endoscope System for Future Application in Minimally Invasive Laser Osteotomy: First Concept Evaluation”, IEEE Transactions on Medical Robotics and Bionics, vol. 4, núm. 3, pp. 621–633, ago. 2022, doi: 10.1109/TMRB.2022.3172471.

[9] G. Solís-Perales, S. Bowong, y R. Femat, “SYNCHRONIZATION OF DYNAMICAL SYSTEMS WITH DIFFERENTE ORDER AND TOPOLOGY”, IFAC Proceedings Volumes, vol. 39, núm. 8, pp. 154–159, ene. 2006, doi: 10.3182/20060628-3-FR-3903.00029.

[10] H. Nijmeijer y A. Rodriguez-Angeles, “Synchronization of Mechanical Systems”, en World Scientific Series on Nonlinear Science Series A, vol. 46. WORLD SCIENTIFIC, sep. 2003. doi: 10.1142/5391.

[11] J. P. Ramirez y H. Nijmeijer, “The secret of the synchronized pendulums”, Phys. World, vol. 33, núm. 1, p. 36, ene. 2020, doi: 10.1088/2058-7058/33/1/28.

[12] J. A. S. Kelso, “Unifying Large- and Small-Scale Theories of Coordination”, Entropy (Basel), vol. 23, núm. 5, p. 537, abr. 2021, doi: 10.3390/e23050537.