


Sánchez, C.J. RSCTyH, VOL. I, No.01, Enero 2023
Resumen: En este trabajo, se expone una forma segura de transmisión de varias señales basada en la sincronización del caos. La idea es transmitir de un modo seguro tantas señales como la cantidad de estados del sistema caótico lo permita. Se requiere que el atractor caótico transmitido no cambie para mantener el nivel de seguridad. El método se basa en la teoría de control de múltiples entradas y múltiples salidas (MIMO) para sistemas no lineales. Además, el Transmisor y el Receptor se sincronizan a pesar de las incertidumbres en ambos sistemas. En este sentido, el esquema de comunicación segura es robusto. Se ilustra el resultado utilizando la sincronización de sistemas similares Palabras claves: Sincronización de Caos, Transmisión Segura Robusta,Control No Lineal.a |
Abstract: In this contribution, we present the secure transmission of several signals based on chaos synchronization. The idea is to transmit as many signals as the system states in a secure manner. It is required that the transmitted chaotic attractor must not change to maintain the security level. The method is based on the Multiple-Input and Multiple-Output (MIMO) control theory for nonlinear systems. Moreover, the Transmitter and Receiver synchronize in spite of the uncertainties in both systems. In this sense, the secure communication scheme is robust. We illustrate the result using the synchronization of similar systems. Keywords: Chaos Synchronization, Robust Secure Transmission, Nonlinear Control. |
Recibido:17/10/22; Aceptado: 12/12/2022; Publicado 25/01/2023
Introduction
In the last two decades, the synchronization problem of chaotic systems has been widely studied, see, for instance, [1], [2], and [3]. The reasons for the interest in this problem are the potential applications and the synchronization phenomena. The main application is secure communication, where it is proved that relevant information can be transmitted and recovered using chaotic synchronization, and it has been demonstrated that the method is feasible, see for example, [4] and [5]. The other main interest is the dynamical phenomena of synchronization, where some relevant efforts have been made [6], [7], from where some open problems persist. For instance, one problem is the synchronization of strictly different systems, and the other is the synchronization of dynamical systems with different order [8]. The former deal with the problem of synchronize two systems whose models come from two different phenomena. The latter concerns the synchronization of dynamical systems that evolves in different spaces, in other words, a system with nonequal dimension. Synchronization of strictly different systems is still a problem under investigation.
Secure communication is understood as the transmission of signals or messages masked or hidden into the chaotic attractor of the transmitter system. Then the Receiver provides the transmitted signal or message via a particular unmasking algorithm. In this manner a simplex communication scheme is constructed; however, until the authors' knowledge, the secure transmission schemes consist in transmitting a single message or signal provided that the signal does not destroy the chaotic behavior of the transmitter. Several chaos-based communication schemes have been published. Among these, two basic configurations can be identified. (i) An approach consists of adding the signal to the chaotic carrier, which is transmitted to the receiver. That is, the master system comprises the full-state model, whereas the slave system is composed of a reduced model, and the transmitted state completes the receiver system. (ii) Another transmitter/receiver design is based on the full state model of the driving and response systems [9]. That is, both drive and response systems are represented by dynamical systems of the same order. The homogeneous-synchronization configuration has been recently addressed via parameter modulation. Kocarev and Parlitz have proposed a generalization of these approaches, which extends the capabilities for constructing synchronized systems. Their approach enables the message signal to be integrated as a driving signal. However, the message signal can be recovered only under ideal conditions [10].
In this report, we illustrate that multiple signals can be transmitted using a single transmitter system and a single receiver using nonlinear Multiple-Input and Multiple-Output control techniques. In this way, a stereo audio signal can be transmitted, or different conversations can be embedded to be transmitted at the same time. Moreover, chaotic behavior should be maintained.
The control strategy is based on a diffeomorphic transformation obtained from the derivatives of the output functions along the system vector fields for a single signal see [5]. Then as the transmitter system poses many inputs as transmitted signals, it is required the same number of control inputs in the receiver in order to recover each signal.
The writing is organized as follows: Section 2, presents the secure communication based on robust synchronization of similar chaotic systems, in Section 3 an application for secure communication is illustrated and finally Section 4 presents the conclusions of the work.
Materials and Methods
The key procedure consists in synchronize chaotic systems with same order and model. To this end, we consider chaotic systems in the following form
Ec. 1
where vector fields  are sufficiently smooth and similar, with
are sufficiently smooth and similar, with  being the attraction region,
being the attraction region,  ,
,  are the input vectors with
are the input vectors with  being unknown and
being unknown and  ,
,  are the real-valued output functions,
are the real-valued output functions,  are the signals to be transmitted and the signals
are the signals to be transmitted and the signals  stand for the control signals to achieve synchronization, and once the systems are synchronous, the recovered messages are reproduced by the control command signals. These considerations define a Multiple-Input and Multiple-output system.
stand for the control signals to achieve synchronization, and once the systems are synchronous, the recovered messages are reproduced by the control command signals. These considerations define a Multiple-Input and Multiple-output system.
Therefore, we use the nonlinear control theory for MIMO systems. To begin with, from Master and Slave systems, the synchronization error system is given as
Ec. 2
where  is the state vector of the synchronization error system,
is the state vector of the synchronization error system,  ,
, 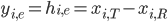 . The underlying idea of the nonlinear feedback control is to find functions
. The underlying idea of the nonlinear feedback control is to find functions  such that the desired dynamical behavior is induced for any initial condition
such that the desired dynamical behavior is induced for any initial condition  in an attraction basin
in an attraction basin  . Then, from the Lie-based geometric approach, it is possible to find a transformation
. Then, from the Lie-based geometric approach, it is possible to find a transformation  , for
, for 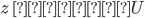 , such that the affine form of the synchronization error system takes a linearizable canonical form. We depart from the relative degree definition for a MIMO system [11].
, such that the affine form of the synchronization error system takes a linearizable canonical form. We depart from the relative degree definition for a MIMO system [11].
Definition 1. The Multiple Input and Multiple Output affine system (2) has the relative degree vector  at the point
at the point  if:
if:
 , for all
, for all  ,
,  ,
,  , and for all
, and for all  in the neighborhood of
in the neighborhood of 
 matrix
matrix Ec. 3
is nonsingular at  .
.
Remark 1. The previous definition of the relative degree is for a system with the same number of inputs signals as output signals. Therefore, the relative degree matrix  is square.
is square.
Suppose that the system (2) gives  , then the matrix
, then the matrix  is given as follows
is given as follows
c.4
Due to the invertibility of the matrix  , a diffeomorphic transformation can be determined. Such a transformation is given by
, a diffeomorphic transformation can be determined. Such a transformation is given by  , since the relative degree
, since the relative degree  the linearizable system is given by
the linearizable system is given by
 Ec. 5
Ec. 5
where  and
and  . Thus, from (5) the linearizing controllers are given by
. Thus, from (5) the linearizing controllers are given by
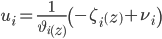 Ec. 6
Ec. 6
Where 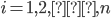 and
and  is the new control that leads the system state to a prescribed reference, in this case, it leads the trajectories of the system (2) to the origin.
is the new control that leads the system state to a prescribed reference, in this case, it leads the trajectories of the system (2) to the origin.
Remark 2. The controller (6) is the so-called perfect control since it requires the perfect knowledge of the functions  and
and  , in order to accomplish the synchronization.
, in order to accomplish the synchronization.
At this point, we can assume the following:
Assumption 1. Only the state vector  is available for feedback.
is available for feedback.
Assumption 2.  is an injective function, bounded away from zero.
is an injective function, bounded away from zero.
Assumption 3. There exists a scalar function  available for feedback such that
available for feedback such that 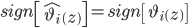 at any
at any  of
of  .
.
Thus, for a realistic case, we consider that these functions are unknown, in seek of clarity  represents the way as the control input is affecting the system and
represents the way as the control input is affecting the system and  represents the dynamics that should be compensated (uncertain terms and parameters as well as the transmitted signals). These unknown functions represent a source of uncertainty due to parameters and non-modeled dynamics. Moreover, if there exist external perturbations or systems faults, they appear in function
represents the dynamics that should be compensated (uncertain terms and parameters as well as the transmitted signals). These unknown functions represent a source of uncertainty due to parameters and non-modeled dynamics. Moreover, if there exist external perturbations or systems faults, they appear in function  or
or  . For these reasons, the controllers (6) are not physically realizable. To overcome this problem, we propose a representation that lumps the uncertain terms into a new uncontrollable but observable state variable. Following ideas reported in [12], [13] and [14], the system (5) can be written in an extended form by defining
. For these reasons, the controllers (6) are not physically realizable. To overcome this problem, we propose a representation that lumps the uncertain terms into a new uncontrollable but observable state variable. Following ideas reported in [12], [13] and [14], the system (5) can be written in an extended form by defining  ,
,  , note that
, note that  lumps the uncertainties. Now, let us define
lumps the uncertainties. Now, let us define  . Thus, the system (5) takes the form
. Thus, the system (5) takes the form
Ec. 7
where , the augmented state
 provides the dynamics of the uncertain function
provides the dynamics of the uncertain function  , therefore, the system (7) is dynamically equivalent to system (5). Thus the
, therefore, the system (7) is dynamically equivalent to system (5). Thus the  th linearizing-like control law is modified in the following form
th linearizing-like control law is modified in the following form
 Ec. 8
Ec. 8
function  is an estimate of the function
is an estimate of the function  and can be used provided that
and can be used provided that 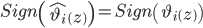 [14]. Notice that the sign should be constant since any change of sign in function
[14]. Notice that the sign should be constant since any change of sign in function  implies a zero crossing, and the matrix
implies a zero crossing, and the matrix  losses invertibility. Then under the linearizing control feedback (8), the states
losses invertibility. Then under the linearizing control feedback (8), the states  converge to zero. Since the feedback controller yield bounded trajectories of state
converge to zero. Since the feedback controller yield bounded trajectories of state 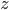 , thus
, thus  is also bounded for all
is also bounded for all  . More precisely, if
. More precisely, if  converges to an equilibrium point, then
converges to an equilibrium point, then  also converges to an equilibrium point. Therefore, under feedback (8), the states of system (7) converge asymptotically to zero.
also converges to an equilibrium point. Therefore, under feedback (8), the states of system (7) converge asymptotically to zero.
It is important to stress that the controller (8) is not realizable since the new state  is unknown. Therefore, a state estimator is proposed to estimate the uncertain states, which is given as follows
is unknown. Therefore, a state estimator is proposed to estimate the uncertain states, which is given as follows
Ec. 9
where  and
and  are tuning parameters chosen in such way that the estimated values
are tuning parameters chosen in such way that the estimated values  .
.
Proposition 1. Let  be an estimation error vector whose components are defined as:
be an estimation error vector whose components are defined as:  and
and  . For sufficiently large
. For sufficiently large  , the dynamics of the estimation error decays globally exponentially to zero if
, the dynamics of the estimation error decays globally exponentially to zero if 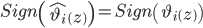 .
.
Proof: Combining systems (7) and (9) the dynamics of the estimation error can be written as follows
 Ec. 10
Ec. 10
where  and the matrix
and the matrix 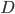 is
is
 Ec. 11
Ec. 11
in which  and
and  which implies
which implies 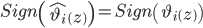 thus
thus 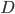 is obviously Hurwitz. There exists a positive definite and symmetric matrix
is obviously Hurwitz. There exists a positive definite and symmetric matrix  such that
such that  where
where  is the identity matrix of dimension 2. Choosing
is the identity matrix of dimension 2. Choosing  as a the Lyapunov like function candidate, one has
as a the Lyapunov like function candidate, one has
Ec. 12
Let  be the estimation error. The function
be the estimation error. The function  satisfies
satisfies  and
and  for some
for some  and
and  , respectively. Thus,
, respectively. Thus,  is a certain bounded function. Moreover, let
is a certain bounded function. Moreover, let  be satisfied for some positive constant
be satisfied for some positive constant  . In this way, we have
. In this way, we have
 Ec. 13
Ec. 13
so that  tends to a set bounded by
tends to a set bounded by  . The dependence on the estimation error
. The dependence on the estimation error  on
on  deserves special attention. Note that as
deserves special attention. Note that as  increases,
increases,  will decrease, which also decreases the exponential estimation error bound. This argument shows that with the proposed method,
will decrease, which also decreases the exponential estimation error bound. This argument shows that with the proposed method,  should be made as large as possible and this achieves the proof.
should be made as large as possible and this achieves the proof.
The previous proposition states that there exists a Lyapunov function that depends on parameter  and provides the global exponential convergence of the estimation error dynamics. With the estimates of the states, the linearizing control low can be modified as follows
and provides the global exponential convergence of the estimation error dynamics. With the estimates of the states, the linearizing control low can be modified as follows
 Ec. 14
Ec. 14
An important characteristic is that this feedback only uses estimated values of the uncertain terms, which gives the feature of robust feedback, moreover it only requires the measure of the output states.
Thus, the Robust Control Scheme for hyperchaotic synchronization can be achieved by means of the state estimator (9) and the robust feedback (14). In this sense, it is required that the state estimator converges to the corresponding states. This result can be stated in the following proposition.
Proposition 2. Consider two chaotic/hyperchaotic systems with a synchronization error given by the system (2). The system (2) converges asymptotically to zero under the feedback (14) via the stabilization of the extended system (7).
Proof: Substituting the robust feedback (14) into (7) and considering the estimation error system (10), the closed-loop dynamics is given by
Ec. 15
Since  and
and  it follows that
it follows that  (which can be computed from the first integral of
(which can be computed from the first integral of  , i.e.,
, i.e.,  . Then, according to the Contraction Mapping Theorem, the state
. Then, according to the Contraction Mapping Theorem, the state  can be expressed globally and uniquely as a function of the coordinates
can be expressed globally and uniquely as a function of the coordinates 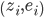 . Now, note that since the matrix
. Now, note that since the matrix 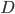 is Hurwitz by construction, and the nonlinear function
is Hurwitz by construction, and the nonlinear function  is bounded, the estimation error system (15) is asymptotically stable. In this sense, given a compact set of initial conditions
is bounded, the estimation error system (15) is asymptotically stable. In this sense, given a compact set of initial conditions  containing the origin, there exists an upper bound
containing the origin, there exists an upper bound  such that
such that  and a high gain estimator parameter
and a high gain estimator parameter  such that
such that  is contained into the attraction basin. Hence, the closed-loop system is semi-globally practically stable, i.e.,
is contained into the attraction basin. Hence, the closed-loop system is semi-globally practically stable, i.e.,  , and this achieves the proof.
, and this achieves the proof.
Therefore, with these results, one can design controllers that achieve synchronization in spite of uncertainties. Thus, we apply these results to construct a secure communication system based on synchronization.
Results and Discussion
To illustrate our proposal, we consider two chaotic Rössler systems given by
Ec. 16
one for the Transmitter and the other for the Receiver. For this case, the parameters were considered equal in both systems. Then we desire to send three signals without excessive deformation or destroy the chaotic Transmitter attractor. In this example we transmit a square periodic signal and two sinusoids, all with different amplitudes and frequencies. Once the signals have been injected into the Transmitter system, the attractor of the Transmitter is illustrated in Figure 1, where there is a slight deformation of the attractor, and it still provides a chaotic behavior.
Figure 1. Chaotic attractor for the Rössler Transmitter system when the transmitted signals are injected.
Therefore, the synchronization error system obtained from the Transmitter and Receiver system is given by
Ec. 17
where the function  stands for the terms given by the nonlinear operation between systems. As was stated in the previous section, system (17) is a nonlinear Multiple-Input and Multiple-Output one, moreover the relative degree matrix
stands for the terms given by the nonlinear operation between systems. As was stated in the previous section, system (17) is a nonlinear Multiple-Input and Multiple-Output one, moreover the relative degree matrix  which is invertible and satisfies the propositions of the previous section. Following the corresponding procedure, one has that the diffeomorphic transformation is given by
which is invertible and satisfies the propositions of the previous section. Following the corresponding procedure, one has that the diffeomorphic transformation is given by  . Once we have the transformation, the system for the synchronization error can be written as
. Once we have the transformation, the system for the synchronization error can be written as
Ec. 18
where the function  comprises the uncertain terms since it represents the derivatives of the
comprises the uncertain terms since it represents the derivatives of the  th output along the vector field of the synchronization error system and the function
th output along the vector field of the synchronization error system and the function  stands for the function of the input control and is considered uncertain, but by Assumption 3 there exists an estimated value given by
stands for the function of the input control and is considered uncertain, but by Assumption 3 there exists an estimated value given by  . Therefore, we can calculate the controllers as follows
. Therefore, we can calculate the controllers as follows
 Ec. 19
Ec. 19
where the new dynamic is given by  , however as was discussed above, the function
, however as was discussed above, the function  is uncertain and the previous controller is not realizable. The idea is to lump the uncertain terms into a new state. Thus, the transformed system can be extended as follows
is uncertain and the previous controller is not realizable. The idea is to lump the uncertain terms into a new state. Thus, the transformed system can be extended as follows
Ec. 20
This new system does not have the uncertainties of the synchronization error system; however, it has new states that provide the dynamic of the uncertainties. Again, the new states are not available from the system but can be estimated to have an estimated value, and the controllers can counteract them.
The state estimators for system (20) are given by
Ec. 21
where this estimator provides the corresponding estimated values of the uncertain states  . With these estimates, we have that the controllers are given by
. With these estimates, we have that the controllers are given by
 Ec. 22
Ec. 22
Therefore, it is possible to determine the estimators and controller gains such that the closed-loop systems be stable, and applying these controllers to the corresponding systems, we obtain that the synchronization is achieved as illustrated in Figure 2, where the controllers were activated at  sec., after that the signals were applied or transmitted for
sec., after that the signals were applied or transmitted for  sec. Thus, it is observed that neither the chaotic attractor nor the synchronization is affected considerably when the signals are injected.
sec. Thus, it is observed that neither the chaotic attractor nor the synchronization is affected considerably when the signals are injected.
Figure 2. Synchronization of the Transmitter and Receiver systems, at  sec. the synchronization is initiated, whereas for
sec. the synchronization is initiated, whereas for  sec. the signals are injected into the Transmitter system.
sec. the signals are injected into the Transmitter system.
Once the chaotic synchronization and the signals have been injected, the recovered transmitted signals are presented in Figure 3.
Note that the recovered signals are very close to the transmitter. Therefore, digital and analogous signals can be transmitted simultaneously in a secure way in spite of uncertainties in the Transmitter and Receiver systems.
Figure 3. Transmitted and recovered signals.
Conclusions
In this contribution, we presented that using chaos synchronization, multiple signals can be transmitted in a secure way. The proposal is such that analog and digital signals can be transmitted without deforming or destroying the chaotic behavior of the Transmitter and Receiver. Also, we considered the case when the controllers do not pose full information about the controlled system, in this way, the communication scheme is robust against unknown parameter values or external (signal transmitted) perturbations. The scheme is general for  order systems, therefore, in principle, it can be used to transmit
order systems, therefore, in principle, it can be used to transmit  signals. The key assumption was that the systems are similar and the parameter variations were not considered, but it is being an understudy.
signals. The key assumption was that the systems are similar and the parameter variations were not considered, but it is being an understudy.
Conflicts of Interest
The authors solemnly declare that we are not and shall not be in any situation which could give rise to a conflict of interest.
References
[1] L. M. Pecora and T. L. Carroll, “Synchronization in chaotic systems,” Phys ical review letters, vol. 64, no. 8, p. 821, 1990.
[2] S. Boccaletti, J. Kurths, G. Osipov, D. Valladares, and C. Zhou, “The synchronization of chaotic systems,” Physics reports, vol. 366, no. 1-2, pp. 1–101, 2002.
[3] A. Pikovsky, M. Rosenblum, and J. Kurths, “Synchronization: a universal concept in nonlinear science,” 2002.
[4] K. M. Cuomo and A. V. Oppenheim, “Circuit implementation of synchronized chaos with applications to communications,” Physical review letters, vol. 71, no. 1, p. 65, 1993.
[5] R. Femat, R. Jauregui-Ortiz, and G. Solís-Perales, “A chaos-based communication scheme via robust asymptotic feedback,” IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, vol. 48, no. 10, pp. 1161–1169, 2001.
[6] R. Femat and G. Solís-Perales, “On the chaos synchronization phenomena,” Physics Letters A, vol. 262, no. 1, pp. 50–60, 1999.
[7] R. Brown and L. Kocarev, “A unifying definition of synchronization for dynamical systems,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 10, no. 2, pp. 344–349, 2000.
[8] R. Femat and G. Solís-Perales, “Synchronization of chaotic systems with different order,” Physical Review E, vol. 65, no. 3, p. 036226, 2002.
[9] C. W. Wu and L. O. Chua, “A simple way to synchronize chaotic systems with applications to secure communication systems,” International Journal of Bifurcation and Chaos, vol. 3, no. 06, pp. 1619–1627, 1993.
[10] L. Kocarev and U. Parlitz, “General approach for chaotic synchronization with applications to communication,” Physical review letters, vol. 74, no. 25, p. 5028, 1995.
[11] A. Isidori, Nonlinear control systems: an introduction. Springer, 1985. Boccaletti, S., Kurths, J., Osipov, G., Valladares, D. L., & Zhou, C. S. (2002). The synchronization of chaotic systems. Physics reports, 366(1-2), 1-101.
[12] R. Femat, “An extension to chaos control via lie derivatives: fully linearizable systems,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 12, no. 4, pp. 1027–1033, 2002.
[13] R. Femat, J. Alvarez-Ramirez, B. Castillo-Toledo, and J. Gonzalez, “On robust chaos suppression in a class of nondriven oscillators: application to the chua’s circuit,” IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, vol. 46, no. 9, pp. 1150–1152, 1999.
[14] R. Femat, J. Alvarez-Ramírez, and G. Fernández-Anaya, “Adaptive synchronization of high-order chaotic systems: a feedback with low-order parametrization,” Physica D: Nonlinear Phenomena, vol. 139, no. 3-4, pp. 231–246, 2000.